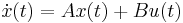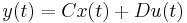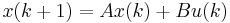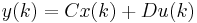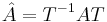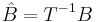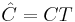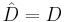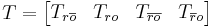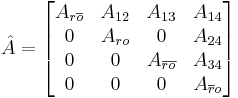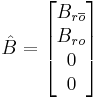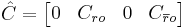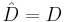Kalman decomposition
Kalman decomposition provides a mathematical means to convert a representation of any linear time-invariant control system to a form in which the system can be decomposed into a standard form which makes clear the observable and controllable components of the system. This decomposition results in the system being presented with a more illuminating structure, making it easier to draw conclusions on the system's reachable and observable subspaces.
Contents |
Notation
The derivation is identical for both discrete-time as well as continuous time LTI systems. The description of a continuous time linear system is
where
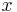 is the "state vector",
is the "state vector",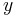 is the "output vector",
is the "output vector",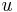 is the "input (or control) vector",
is the "input (or control) vector",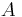 is the "state matrix",
is the "state matrix",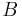 is the "input matrix",
is the "input matrix",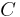 is the "output matrix",
is the "output matrix",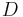 is the "feedthrough (or feedforward) matrix".
is the "feedthrough (or feedforward) matrix".
Similarly, a discrete-time linear control system can be described as
with similar meanings for the variables. Thus, the system can be described using the tuple consisting of four matrices 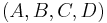 . Let the order of the system be
. Let the order of the system be 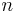 .
.
Then, the Kalman decomposition is defined as a transformation of the tuple 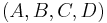 to
to 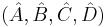 as follows:
as follows:
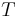 is an
is an 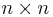 invertible matrix defined as
invertible matrix defined as
where
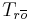 is a matrix whose columns span the subspace of states which are both reachable and unobservable.
is a matrix whose columns span the subspace of states which are both reachable and unobservable.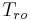 is chosen so that the columns of
is chosen so that the columns of 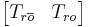 are a basis for the reachable subspace.
are a basis for the reachable subspace.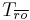 is chosen so that the columns of
is chosen so that the columns of 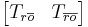 are a basis for the unobservable subspace.
are a basis for the unobservable subspace.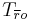 is chosen so that
is chosen so that 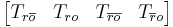 is invertible.
is invertible.
By construction, the matrix 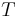 is invertible. It can be observed that some of these matrices may have dimension zero. For example, if the system is both observable and controllable, then
is invertible. It can be observed that some of these matrices may have dimension zero. For example, if the system is both observable and controllable, then 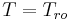 , making the other matrices zero dimension.
, making the other matrices zero dimension.
Standard Form
By using results from controllability and observability, it can be shown that the transformed system 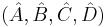 has matrices in the following form:
has matrices in the following form:
This leads to the conclusion that
- The subsystem
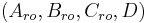 is both reachable and observable.
is both reachable and observable. - The subsystem
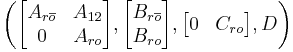 is reachable.
is reachable. - The subsystem
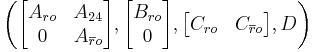 is observable.
is observable.
See also
External links
- Lectures on Dynamic Systems and Control, Lecture 25 - Mohammed Dahleh, Munther Dahleh, George Verghese — MIT OpenCourseWare